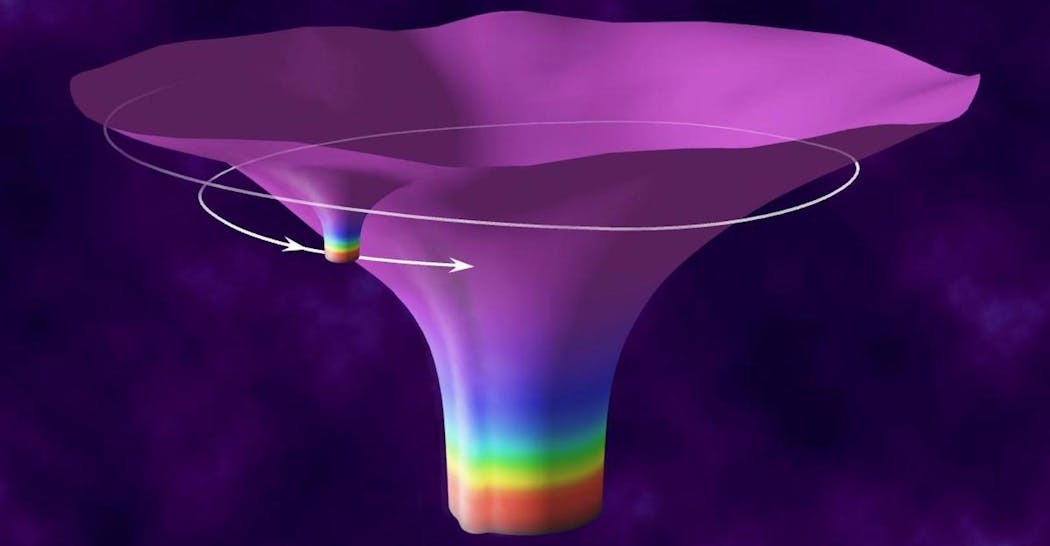
Schematic: Extreme mass-ratio inspiral system, where a small black hole continuously perturbs the gravitational field of a large black hole to generate gravitational waves.

Gravitational waves are often described as ripples in spacetime. Just as a fish thrashing in a calm pond creates ripples that spread across the water's surface, the violent motion of black holes can also stir spacetime, generating these ripples—gravitational waves. One way to make a black hole produce gravitational waves is by perturbing it, which can be likened to imagining the black hole as a musical instrument and "plucking" it to generate waves. This perturbation can be achieved by directly colliding with the black hole or acting upon it from a distance, as the black hole severely warps the spacetime around it, allowing disturbance without direct contact. A typical scenario is when a smaller black hole orbits a central, much larger black hole (known as an extreme mass-ratio inspiral, EMRI), continuously "playing" the larger black hole and producing gravitational waves.

To calculate the gravitational waves produced in such typical scenarios, scientists have developed the theory of black hole perturbation for research. However, precisely and efficiently using black hole perturbation theory to compute gravitational waves remains a challenge. Currently, the most common black holes in astrophysics are spinning Kerr black holes, whose perturbations are described by the Teukolsky equation. For calculating the homogeneous solutions to this equation, there have primarily been two main methods. One is the Sasaki-Nakamura method, which transforms the equation to overcome its shortcomings over long distances, then solves it using finite difference methods. The other is the semi-analytical Mano-Suzuki-Takasugi method, which constructs homogeneous solutions using hypergeometric functions. Current mainstream algorithms worldwide for computing gravitational waves from EMRIs are largely based on these two methods, such as those in the Black Hole Perturbation Toolkit developed by the team for the LISA (Laser Interferometer Space Antenna) space gravitational-wave detection mission initiated by the European Space Agency.

However, both methods have certain drawbacks. The former suffers from low accuracy and efficiency due to its reliance on numerical integration. The latter, while fast and accurate, has poor convergence—or even fails to converge—for cases with larger frequencies. These limitations hinder scientists' ability to rapidly generate high-precision gravitational waveforms. Addressing this challenge, the research group led by Wenbiao Han at the Shanghai Astronomical Observatory has proposed a new algorithm based on series expansion for solving the Teukolsky equation in black hole perturbation theory. Following convention, this method has been named the Jiang-Han algorithm. "The new algorithm is tens to hundreds of times faster than the mainstream algorithms in the international Black Hole Perturbation Toolkit while maintaining the same accuracy," explained Ye Jiang, the first author of the paper and a Ph.D. student at Shanghai Astronomical Observatory. "Crucially, our algorithm can be applied to arbitrary frequency ranges, even complex frequencies."

Currently, Han's group has built a fully relativistic gravitational wave calculation model for asymmetric binary systems based on this new method, which is now the most precise and fastest fully relativistic waveform template. This template can be directly applied to data analysis for China's future space-based gravitational wave detection missions.

Paper Link:https://journals.aps.org/prd/abstract/10.1103/kkmt-fbjb

Scientific Contacts: Ye Jiang, Wenbiao Han (wbhan@shao.ac.cn)